Mehrstufige Logik
Mit dem etwas flapsigen Begriff "Mehrstufige Logik" fasse ich alle Methoden zusammen, bei denen man sich Zwischenergebnisse merkt, mit denen man selbst noch keine Zahl platzieren kann, die aber dabei helfen können, an anderer Stelle eine Zahl zu platzieren.
Hier ein kleines Beispiel:
-
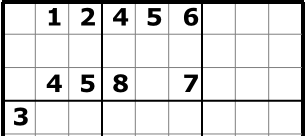
- Ein Ausschnitt aus einem Sudoku, bei man die Drei nur mit mehrstufiger Logik platzieren kann.
Obwohl nur eine einzige Drei im gezeigten Ausschnitt gegeben ist, reicht sie, um eine weitere Drei platzieren zu können.
Dazu muss man sich den linken 3x3-Block anschauen:
-
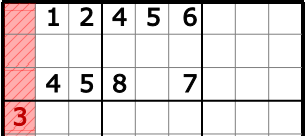
- Im linken 3x3-Block kann die Drei nicht ganz links auftauchen.
Dort kann man noch keine Drei platzieren, aber man kann sich merken, dass sie in der Mitte oder rechts auftauchen muss:
-
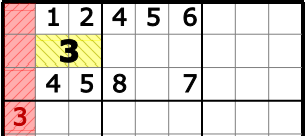
- Im linken 3x3-Block kann die Drei nur in der Mitte oder rechts stehen.
Damit weiß man aber auch, dass in der zweiten Zeile eine Drei im linken Block auftauchen muss und in dem Rest der Zeile nicht mehr vorkommen kann:
-
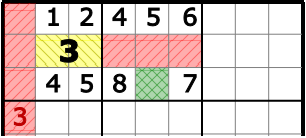
- In der mittleren Zeile steht im linken 3x3-Block bereits eine Drei, im Rest der Zeile kann keine mehr sein. Damit gibt es im mittleren 3x3-Block nur noch eine Stelle für die Drei.
Mit diesem Wissen kann man im mittleren 3x3-Block die 3 platzieren:
-
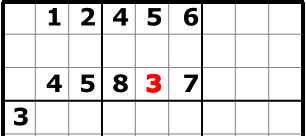
- Der Sudokuausschnitt mit der neu gefunden Drei (graue Schrift).